Pretty Rubik´s Cube patterns with algorithms
Are you tired of solving your Rubik´s Cube always the same way or are you looking for a new challenge? Try to reproduce or invent some pretty patterns! In this section I´m going to present some of my favorite Rubik´s Cube patterns algorithms with preview images, like the famous Superflip, the checkerboard, the snake patterns, the cross, the cube in a cube and other nice motives. If you got bored solving the Rubik’s Cube always the same way and want new challenge try to reach one of these patterns without watching the algorithms supplied.
In case you don´t know what these letters mean you should get started by reading the Rubik´s notation. If you don´t have a Magic Cube go ahead and use the online Rubik´s Cube solver program where you can apply rotations or even solve the cube online.
In case you don´t know what these letters mean you should get started by reading the Rubik´s notation. If you don´t have a Magic Cube go ahead and use the online Rubik´s Cube solver program where you can apply rotations or even solve the cube online.
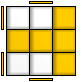
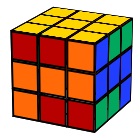
The Superflip
U R2 F B R B2 R U2 L B2 R U’ D’ R2 F R’ L B2 U2 F2
The SuperFlip is the “most scrambled” Rubik’s Cube pattern. Every piece is where it’s supposed to be but the edges are oriented wrong. Computer programs need the highest amount of steps (20) to solve this state.
The SuperFlip is the “most scrambled” Rubik’s Cube pattern. Every piece is where it’s supposed to be but the edges are oriented wrong. Computer programs need the highest amount of steps (20) to solve this state.
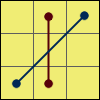
The Checkerboard
F B2 R’ D2 B R U D’ R L’ D’ F’ R2 D F2 B’:
Corner pieces are in place, oriented the correct way, but the edges are shifted to the the adjacent face to form this nice-looking design.

F B2 R’ D2 B R U D’ R L’ D’ F’ R2 D F2 B’:
Corner pieces are in place, oriented the correct way, but the edges are shifted to the the adjacent face to form this nice-looking design.
The easy checkerboard

M2 E2 S2
( = U2 D2 F2 B2 L2 R2)
The most simple algorithm, it only takes three double layer moves to make it.

M2 E2 S2
( = U2 D2 F2 B2 L2 R2)
The most simple algorithm, it only takes three double layer moves to make it.
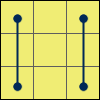
Wire
(R L F B) x 3 – R2 B2 L2 R2 B2 L2

(R L F B) x 3 – R2 B2 L2 R2 B2 L2
Tablecloth

R L U2 F’ U2 D2 R2 L2 F’ D2 F2 D R2 L2 F2 B2 D B2 L2

R L U2 F’ U2 D2 R2 L2 F’ D2 F2 D R2 L2 F2 B2 D B2 L2
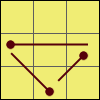
Spiral pattern
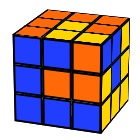
L’ B’ D U R U’ R’ D2 R2 D L D’ L’ R’ F U
Looks great on bigger puzzles

L’ B’ D U R U’ R’ D2 R2 D L D’ L’ R’ F U
Looks great on bigger puzzles
Speedsolving.Com Logo
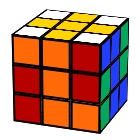
R’ L’ U2 F2 D2 F2 R L B2 U2 B2 U2

R’ L’ U2 F2 D2 F2 R L B2 U2 B2 U2
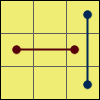
Vertical stripes
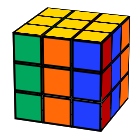
F U F R L2 B D’ R D2 L D’ B R2 L F U F

F U F R L2 B D’ R D2 L D’ B R2 L F U F
Opposite corners

R L U2 F2 D2 F2 R L F2 D2 B2 D2

R L U2 F2 D2 F2 R L F2 D2 B2 D2
Cross
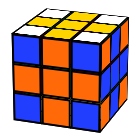
U F B’ L2 U2 L2 F’ B U2 L2 U

U F B’ L2 U2 L2 F’ B U2 L2 U
Cross 2
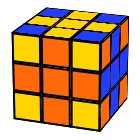
R2 L’ D F2 R’ D’ R’ L U’ D R D B2 R’ U D2

R2 L’ D F2 R’ D’ R’ L U’ D R D B2 R’ U D2
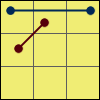
Twisted cube in the big cube
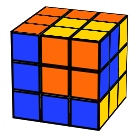
F L F U’ R U F2 L2 U’ L’ B D’ B’ L2 U

F L F U’ R U F2 L2 U’ L’ B D’ B’ L2 U
Cube in a cube in a cube…
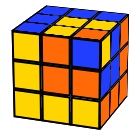
U’ L’ U’ F’ R2 B’ R F U B2 U B’ L U’ F U R F’

U’ L’ U’ F’ R2 B’ R F U B2 U B’ L U’ F U R F’
Anaconda
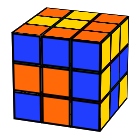
L U B’ U’ R L’ B R’ F B’ D R D’ F’

L U B’ U’ R L’ B R’ F B’ D R D’ F’
Python
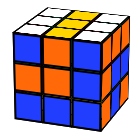
F2 R’ B’ U R’ L F’ L F’ B D’ R B L2

F2 R’ B’ U R’ L F’ L F’ B D’ R B L2
Black Mamba
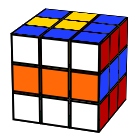
R D L F’ R L’ D R’ U D’ B U’ R’ D’

R D L F’ R L’ D R’ U D’ B U’ R’ D’
Green Mamba

R D R F R’ F’ B D R’ U’ B’ U D2

R D R F R’ F’ B D R’ U’ B’ U D2
Four spots
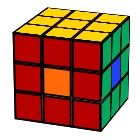
F2 B2 U D’ R2 L2 U D’

F2 B2 U D’ R2 L2 U D’
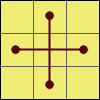
Six spots
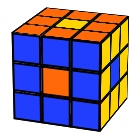
U D’ R L’ F B’ U D’
The same with middle layer turns:
E S E’ S’

U D’ R L’ F B’ U D’
The same with middle layer turns:
E S E’ S’
Twister
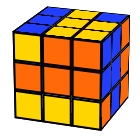
F R’ U L F’ L’ F U’ R U L’ U’ L F’

F R’ U L F’ L’ F U’ R U L’ U’ L F’
Center-Edge-Corner

U’ R2 L2 F2 B2 U’ R L F B’ U F2 D2 R2 L2 F2 U2 F2 U’ F2

U’ R2 L2 F2 B2 U’ R L F B’ U F2 D2 R2 L2 F2 U2 F2 U’ F2
Tetris
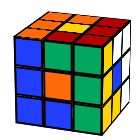
L R F B U’ D’ L’ R’

L R F B U’ D’ L’ R’
Henry’s Zig Zag with Checkerboard
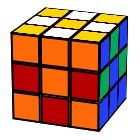
R2 L2 F2 B2 U F2 B2 U2 F2 B2 U

R2 L2 F2 B2 U F2 B2 U2 F2 B2 U
Facing Checkerboards
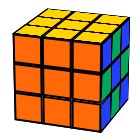
U2 F2 U2 F2 B2 U2 F2 D2

U2 F2 U2 F2 B2 U2 F2 D2


 Mathematicians love the Rubik's cube. There’s no denying it. They are amazed at how such a seemingly simply puzzle can hold so many secrets. There is always something new to learn about the cube (if you are willing to learn, of course). Perhaps the biggest secret of all, one that took over 30 years for mathematicians to crack is God’s Number.
Mathematicians love the Rubik's cube. There’s no denying it. They are amazed at how such a seemingly simply puzzle can hold so many secrets. There is always something new to learn about the cube (if you are willing to learn, of course). Perhaps the biggest secret of all, one that took over 30 years for mathematicians to crack is God’s Number. Perhaps the most famous of the rare scrambles that require exactly 20 moves to solve is the super-flip position (pictured). This is achieved by performing the following sequence of moves – R L U2 F U’ D F2 R2 B2 L U2 F’ B’ U R2 D F2 U R2 U from any orientation. The position is recognisable as every single corner is solved in its place, while every single edge is flipped in its place. This was also the first position that was found that could not be solve in less than 20 moves, raising the lower bound of God’s Number to 20 in 1995.
Perhaps the most famous of the rare scrambles that require exactly 20 moves to solve is the super-flip position (pictured). This is achieved by performing the following sequence of moves – R L U2 F U’ D F2 R2 B2 L U2 F’ B’ U R2 D F2 U R2 U from any orientation. The position is recognisable as every single corner is solved in its place, while every single edge is flipped in its place. This was also the first position that was found that could not be solve in less than 20 moves, raising the lower bound of God’s Number to 20 in 1995.