God’s Number
 Mathematicians love the Rubik's cube. There’s no denying it. They are amazed at how such a seemingly simply puzzle can hold so many secrets. There is always something new to learn about the cube (if you are willing to learn, of course). Perhaps the biggest secret of all, one that took over 30 years for mathematicians to crack is God’s Number.
Mathematicians love the Rubik's cube. There’s no denying it. They are amazed at how such a seemingly simply puzzle can hold so many secrets. There is always something new to learn about the cube (if you are willing to learn, of course). Perhaps the biggest secret of all, one that took over 30 years for mathematicians to crack is God’s Number.
God’s Number, as many cube enthusiasts will already know, is the maximum number of moves required to solve any of the 43,252,003,274,489,856,000 combinations of the cube. It has been proven that this number is 20, however the discovery is fairly recent (July 2010). The term “God’s Number” was coined because the mind of a being able to find the shortest sequence of moves to solve any scramble sequence would have to be thousands of times more powerful than our own, able to test millions of different combinations in the blink of an eye, something that mathematicians believe only a Deity could possess.
This number may seem low, but theoretically it should be even lower. Only around 490,000,000 combinations require the full 20 moves to be solved. Although 490 million is a huge number, it is only a fraction of the 43 quintillion possible combinations (0.0000011328955% to be precise). The chances of generating a random scramble that can only be solved in 20 moves, no more no less, is around 1 in a billion. However, the number of combinations that can be solved in 19 moves is approximately 1.5 quintillion. This means that God’s Number is much closer to 19 than 20, but unfortunately even if only 1 scramble sequence was impossible to solve in less than 20 moves, God’s Number would still be 20.
The Super-Flip

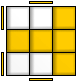
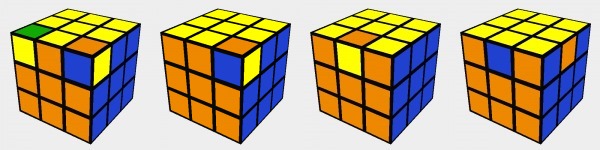
Perhaps the most famous of the rare scrambles that require exactly 20 moves to solve is the super-flip position (pictured). This is achieved by performing the following sequence of moves – R L U2 F U’ D F2 R2 B2 L U2 F’ B’ U R2 D F2 U R2 U from any orientation. The position is recognisable as
every single corner is solved in its place, while every single edge is flipped in its place. This was also the first position that was found that could not be solve in less than 20 moves, raising the lower bound of God’s Number to 20 in 1995.
History of God’s Number
Work began on the search for God’s Number back in 1981, when a man named Morwen Thistlethwaite proved using a complex algorithm he devised himself that 52 moves was enough to solve any of the 43 quintillion different scrambles. This number began to fall slowly as better, more efficient methods were devised for solving the huge number of possible combinations in the fewest moves possible.
Of course, not all 43 quintillion combinations were tested individually by computers. Many ingenious patterns were spotted to reduce this number to a fraction of its original quantity. For example, if you were to perform the super-flip algorithm on a Rubik’s Cube and rotate the entire cube by 180 degrees, you would have theoretically created another of the 43 quintillion combinations without increasing the number of moves required to solve it. The reason for this is because 43 quintillion is the number of positions, not the number of completely unique patterns. If you were to hold the white face on the top and the green face on the front, that would be one position. If you were to rotate the puzzle so you are still holding the white face on the top but instead you had the red face on the front, you would have another position. Therefore, by multiplying the number of different possible “top faces” (6, one for each colour) by the number of different possible “front faces” for each different “top face” (4), you would be left with 24 different ways to position the cube for any given state. This automatically reduces the enormous number of 43 quintillion possible positions that would actually need to be tested to 1,802,166,800,000,000,000 (a mere 4% of the original number). By factoring in other similarities such as mirrors, this number reduces further, making God’s Number much easier to calculate.
 Two different “positions” out of the 43 quintillion possible
Two different “positions” out of the 43 quintillion possible
God’s Number can also be implemented for other twisty puzzle, such as using an original Rubik's cube with certain restraints, or using smaller or bigger puzzles. God’s Number for a Rubik’s Cube solved using only quarter turns (where no face can be rotated more than 90 degrees at a time either clockwise or anticlockwise) has been proven much more recently (2014) to be 26 moves.
God’s Algorithm for 2x2x2 Cubes
God’s Number for the 2x2 puzzle (having only 3,674,160 different positions) has been proven to be 11 moves using the half turn metric, or 14 using the quarter turn metric (half turns count as 2 rotations). Unfortunately God’s Number has yet to be calculated for the 4X4 cube, or higher.
The Devil’s Number
As we have discussed on the Mathematics of the Rubik’s Cube page, every algorithm (permutation) has a degree in group theory. Every sequence of moves, if repeated enough times, will return the cube to the original state. For example a simple face turn needs 4 repetitions, the R' D' R D algorithm needs to be applied six times, going through 24 states.
The question is to find an algorithm which needs the biggest number of repetitions to return to the starting position.
For this we need an algorithm that goes through all 43,252,003,274,489,856,000 possible positions of the cube without repeating any of them. In the mathematical field of graph theory, a Hamiltonian path (also called as traceable path) is a path in a graph that visits each vertex exactly once.
This algorithm is called the Devil’s Algorithm and its length is called the Devil’s Number.
Fewest move challenge in official competitions
In official Rubik's competition organised by World cube Association (WCA), there is an event called Fewest Move Count(FMC), which involves taking a random computer generated scramble and solving it in as few moves as possible. A computer would be able to find more efficient solutions possible that takes the least amount of moves in seconds, however in this event competitors have 1 hour to try and find the most efficient solution that they physically can. The World Record for this event is 20 moves, shared by Tomoaki Okayama (Japan) and Rami Sbahi (USA). These two solves did however take place at two different competitions. Despite the world record coincidentally matching God’s Number, it is almost impossible that either solution to either scramble was the most efficient that could be found by either human or computer.
To conclude, God’s Number is a fascinating theory. It shows us how such a simple looking puzzle can have over 5 and a half times more combinations than there are grains of sand on the Earth, and it also proves that computers will always be infinitely better than humans at almost any task.
Computer programs
The Cube Explorer program by the German mathematician, Herbert Kociemba is able to find the optimal solution in 20 steps using the half turn metric (half turns count as one move). Test our program which is using the same algorithm. It’s looking for the solution in 20 moves but if the program doesn’t return any result below the time threshold then it switches to 24 steps which is also very close to the God’s number.

 Mathematicians love the Rubik's cube. There’s no denying it. They are amazed at how such a seemingly simply puzzle can hold so many secrets. There is always something new to learn about the cube (if you are willing to learn, of course). Perhaps the biggest secret of all, one that took over 30 years for mathematicians to crack is God’s Number.
Mathematicians love the Rubik's cube. There’s no denying it. They are amazed at how such a seemingly simply puzzle can hold so many secrets. There is always something new to learn about the cube (if you are willing to learn, of course). Perhaps the biggest secret of all, one that took over 30 years for mathematicians to crack is God’s Number. Perhaps the most famous of the rare scrambles that require exactly 20 moves to solve is the super-flip position (pictured). This is achieved by performing the following sequence of moves – R L U2 F U’ D F2 R2 B2 L U2 F’ B’ U R2 D F2 U R2 U from any orientation. The position is recognisable as every single corner is solved in its place, while every single edge is flipped in its place. This was also the first position that was found that could not be solve in less than 20 moves, raising the lower bound of God’s Number to 20 in 1995.
Perhaps the most famous of the rare scrambles that require exactly 20 moves to solve is the super-flip position (pictured). This is achieved by performing the following sequence of moves – R L U2 F U’ D F2 R2 B2 L U2 F’ B’ U R2 D F2 U R2 U from any orientation. The position is recognisable as every single corner is solved in its place, while every single edge is flipped in its place. This was also the first position that was found that could not be solve in less than 20 moves, raising the lower bound of God’s Number to 20 in 1995.